Introduction:
The MiniMax algorithm is a fundamental concept for artificial intelligence and game theory, providing a strategic framework for decision-making in two-player, zero-sum games. MiniMax determines optimal moves and outcomes, whether chess, tic-tac-toe, or other competitive games. This post will explore the MiniMax algorithm, understand its mechanics, and develop a practical example to showcase its application.
Understanding MiniMax:
MiniMax is a decision-making algorithm designed for two-player games with a clear winner and loser, often called zero-sum games. These games involve scenarios where one player's gain is equivalent to the other player's loss. The primary objective of MiniMax is to find the best possible move for a player, assuming that the opponent is also playing optimally.
The algorithm recursively explores the game tree, representing all possible moves and their outcomes. Each node in the tree represents a game state, and the edges between nodes represent possible moves. The algorithm assigns scores to each node, indicating the desirability of that particular game state for the player. The scores are determined by evaluating the game's terminal nodes (end states).
Mechanics of MiniMax:
Evaluation Function: At the terminal nodes of the game tree, an evaluation function is applied to determine the utility of that game state. The utility represents the outcome of the game – a positive value for a win, a negative value for a loss, and a zero for a draw.
Backpropagation: The scores are then propagated back up the tree, alternating between maximizing and minimizing players. Maximizing players seek the highest score while minimizing players aim for the lowest score.
Decision Making: The root node's children's scores help the algorithm choose the best move for the player. Maximizing players select the move with the highest score while minimizing players opt for the move with the lowest score.
Example: Tic-Tac-Toe
Let us consider the near-end state of the game, as you can see below. It is X's turn.
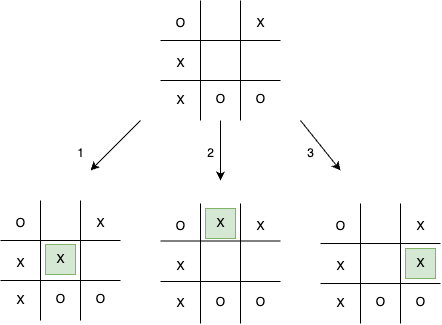
X had three choices, which are marked in green. As you can see, by opting for option 1, X wins, but if we select any other option, there is a possibility that X can win. Remember, we consider that the opponent will also play optimally, so option 1 is.
Now, let's walk through the entire structure. So, we can confirm why option 1 is the best option for X.
In state 1, X generates the states 2, 3 and 4.
State 2 gives us the quickest and surest win for X.
States 3 and 4 are not end state state 3 produces states 5 and 6.
On the other hand, state 4 generates 7 and 8.
In state 5, X loses, which is not our outcome.
Since state 7 from state 4 is undesirable, we will ignore that.
Now, the only options are 6 and 8.
Because it is O's turn in 3 and 4, O will try to find the minimum score; hence, both this state leads to X's loss.
Below is the pseudo-code for minimax.
function MiniMax(board, depth, maximizingPlayer)
if game is over in the current board state
return evaluate the board and return the score
if maximizingPlayer
bestScore = negative infinity
for each valid move in the board
make the move
score = MiniMax(board, depth + 1, false)
undo the move
bestScore = max(bestScore, score)
return bestScore
else
bestScore = positive infinity
for each valid move in the board
make the move
score = MiniMax(board, depth + 1, true)
undo the move
bestScore = min(bestScore, score)
return bestScore
function findBestMove(board, player)
bestMove = null
bestScore = negative infinity
for each valid move in the board
make the move
score = MiniMax(board, 0, false)
undo the move
if score > bestScore
bestScore = score
bestMove = the current move
return bestMoveConclusion:
The MiniMax algorithm is a powerful tool for decision-making in zero-sum games, providing a strategic approach to finding the best moves in various scenarios. While our example focused on tic-tac-toe, MiniMax's principles can be applied to more complex games like chess or checkers. Understanding MiniMax opens the door to exploring advanced artificial intelligence techniques and strategies in competitive gaming.
Comments